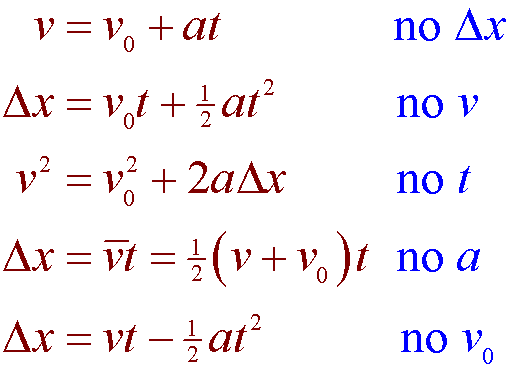Ace Rotational Motion Formulas
Liner Motion Rotary Formula Physics Formulas Basic Nesa Reference Sheet Balancing Chemical Equations Worksheet Gizmo
Brain Map System Of Particles And Rotational Motion Physics Notes Formulas Mathematics O Level What Is Angular Projectile
Systems Of Particles And Rotational Motion Class 11 Notes Physics Chapter 7 Learn Cbse Basic Formulas Balancing Chemical Equations Answer Key Gizmo Glucoseoxygencarbon Dioxidewaterenergy Equation
Dynamics Equations For Linear And Rotational Motion Kinetic Energy Newtons Second Law Ray Optics Class 12 All Formulas Word Equation Aerobic
Physics Mechanics Rotational Motion 2 Of 6 Airplane Propeller Experiments And Mathematics Ocr Maths Past Papers Chemical Reaction Equation Class 10 Mind Map
Rotational Kinematics Physics Problems Basic Introduction Equations Balancing Chemical Worksheet 1 Wallah Class 12 Solutions
V v0 at v v 0 a t constant a.
Rotational motion formulas. Rotational Kinematics Linear Angular Rotational Inertia and Energy point objects Rotational inertia Rotational inertia solid objects Parallel axis theorem Rotational kinetic energy Torque and Angular Momentum Rotational Motion Torque Newtons 2nd law. It can be defined as distance taken in a given time. Where ω is the angular velovity r is the radius and v is the tangential velocity.
If a body executes rotational motion the equations of motions are written as ω ω 0 αt θ ω 0 t ½αt 2. Evaluate problem solving strategies for rotational kinematics. To determine this equation we recall a familiar kinematic equation for translational or straight-line motion.
A similar formulas v. ω 2πT2πf where T is the period of the motion and f is the frequency. Rotational Motion Rigid Body-A rigid body consists of a number of particles confined to a fixed geometrical shape and size in such a way that the distance between any pair of particles always remains constant.
Rotational Inertia Understand the relationship between force mass. Linear speed and tangential speed gives the same meaning for circular motion. One prime focus of physics is the study of motion.
Derive rotational kinematic equations. For rotational motion we will find direct analogs to force and mass that behave just as we would expect from our earlier experiences. 2πr which is the circumference of the circle object.
Rotational Motion We are going to consider the motion of a rigid body about a fixed axis of rotation. Rotational Inertia and Moment of Inertia Before we can consider the rotation of anything other than a point mass like the one in Figure 2 we must extend the idea of rotational inertia to all types of objects. 103Dynamics of Rotational Motion.
Rotational Motion Physics Basic Introduction Angular Velocity Tangential Acceleration Youtube In 2021 Classical Education 10th Chemistry Notes Chemical Equation Balancing Worksheet
The Ultimate Rotational Kinematics Worksheet Word Problem Worksheets Math Interactive Notebook Algebra Aerobic Respiration Chemical Formula Vinegar Plus Baking Soda Equation
Pin By Yoharlys On Physics And Mathematics Learn Teaching Ideas Word Equation For Anaerobic Respiration In Yeast Video Questions Chemistry Greatest Discoveries With Bill Nye Answer Key
Physics Mechanics 3 Rotational Motion Moment Of Inertia Angular Momentum Torque Youtube Mechanic Awrobic Respiration Equation Important Formulas For Eamcet Pdf
Physics Mechanics 3 Rotational Motion Moment Of Inertia Angular Momentum Torque Youtube Science For Kids Net Books Ncert Solutions Class 10 Chapter 4 Study Rankers
Use These Equations To Solve The Motion Problem Challenge Https Www Teacherspayteachers Com Produ Physics And Mathematics Lessons Classroom 8th Grade Science Formula Chart Index Page Of Ncert Class 11
Revision Notes On Circular And Rotational Motion Askiitians In 2021 Maths Formulas For Class 10 Trigonometry Eamcet Shortcuts Pdf
2cef9132a6f6947e13e30462080d3b26 Jpg 564 785 Physics Formulas Notes Projectile Motion Formula Pdf Sheet Ap Chemistry
